largeNum largeNumApplyRoom(largeNum a){
a.number = (int *)malloc(sizeof(int)*a.length);
return a;
}
largeNum initlargeNumber(int length,int *number){
largeNum a;
a.length = length;
a = largeNumApplyRoom(a);
for (int i = 0; i < a.length; i++){
a.number[i] = number[i];
}
return a;
}
largeNum initlargeNumToZero(largeNum a,int length){
a.length = length;
a = largeNumApplyRoom(a);
for (int i = 0; i < a.length; i++) {
a.number[i] = 0;
}
return a;
}
largeNum formatAddZero(largeNum a,int length){
if (length <= a.length ){
return a;
}
largeNum resault;
resault.length = length;
resault = initlargeNumToZero(resault,resault.length);
for (int i = length-1,j = a.length-1; j >= 0 ; i--,j--){
resault.number[i] = a.number[j];
}
return resault;
}
int max(int a,int b){
return a >= b ? a : b ;
}
int min(int a,int b){
return a <= b ? a : b ;
}
int sub(int a,int b){
return max(a,b) - min(a,b);
}
largeNum maxLargeNumLength(largeNum a,largeNum b){
return a.length >= b.length? a : b ;
}
largeNum minLargeNumLength(largeNum a,largeNum b){
return a.length <= b.length? a : b ;
}
largeNum largeNumAdd(largeNum a,largeNum b){
largeNum sum;
if (a.length == b.length){
sum.length = a.length + 1;
sum = initlargeNumToZero(sum,sum.length);
for (int i = a.length - 1; i >= 0; i--){
sum.number[i+1] += (a.number[i]+ b.number[i]);
if (sum.number[i+1] > 9){
sum.number[i] += (sum.number[i+1]/10);
sum.number[i+1] %= 10;
}
}
return sum;
}else{
return largeNumAdd(formatAddZero(minLargeNumLength(a,b),max(a.length,b.length)),maxLargeNumLength(a,b));
}
}
int *largeNumCheckNum(int *a,int length){
for (int i = length-1; i >= 1; i--){
if (a[i] > 9){
a[i-1] += (a[i]/10);
a[i] %= 10;
}
}
if (a[0] > 9){
int *b;
b = (int*)malloc(sizeof(int)*(length+1));
b[0] = a[0]/10;
b[1] = a[0]%10;
for (int j = 2; j < length+1; j++){
b[j] = a[j-1];
}
free(a);
return b;
}
return a;
}
largeNum largeNumMultiply(largeNum a, largeNum b){
largeNum product;
product.length = a.length + b.length;
int **tempProduct;
tempProduct = (int**)malloc(sizeof(int*)*a.length);
for (int t = 0; t < a.length; t++){
tempProduct[t] = (int*)malloc(sizeof(int)*b.length);
}
product = initlargeNumToZero(product,product.length);
for (int j = b.length - 1; j >= 0; j--){
for (int i = a.length - 1; i >= 0; i--){
tempProduct[i][j] = a.number[i] * b.number[j];
product.number[i+j+1] += tempProduct[i][j];
}
}
product.number = largeNumCheckNum(product.number,product.length);
return product;
}
void largeNumPrintf(largeNum a){
int sign = 0;
for (int i = 0; i < a.length; i++){
if (a.number[i] != 0){
sign = 1;
}
if(!sign){
if (i+1 == a.length){
printf("0");break;
}
continue;
}
printf("%d", a.number[i]);
}
}
Matrix initMatrix(largeNum a,largeNum b,largeNum c,largeNum d){
Matrix matrix;
matrix.RowCol00 = a;
matrix.RowCol01 = b;
matrix.RowCol10 = c;
matrix.RowCol11 = d;
return matrix;
}
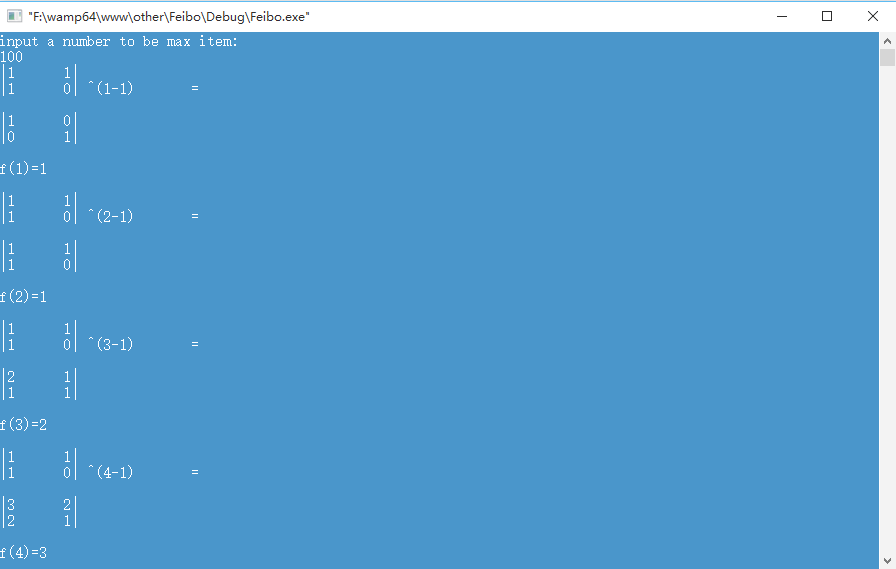
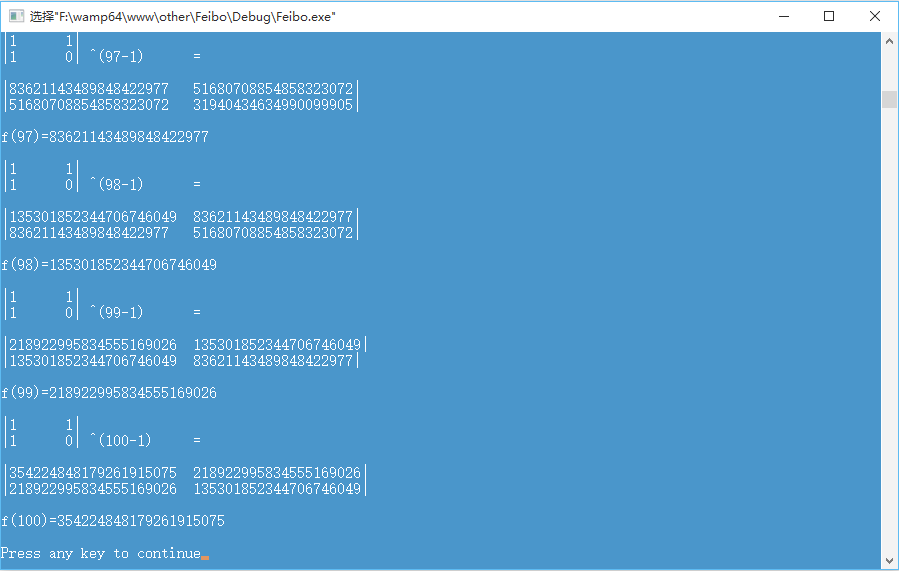
void matrixPrintf(Matrix a){
printf("|");largeNumPrintf(a.RowCol00);printf("\t");largeNumPrintf(a.RowCol01);printf("|\n");
printf("|");largeNumPrintf(a.RowCol10);printf("\t");largeNumPrintf(a.RowCol11);printf("| ");
}
Matrix matrixMultiply(Matrix a,Matrix b){
Matrix product;
product.RowCol00 = largeNumAdd(largeNumMultiply(a.RowCol00,b.RowCol00),largeNumMultiply(a.RowCol01,b.RowCol10));
product.RowCol01 = largeNumAdd(largeNumMultiply(a.RowCol00,b.RowCol01),largeNumMultiply(a.RowCol01,b.RowCol11));
product.RowCol10 = largeNumAdd(largeNumMultiply(a.RowCol10,b.RowCol00),largeNumMultiply(a.RowCol11,b.RowCol10));
product.RowCol11 = largeNumAdd(largeNumMultiply(a.RowCol10,b.RowCol01),largeNumMultiply(a.RowCol11,b.RowCol11));
return product;
}
Matrix matrixPower(matrix a,int n){
if (n==1){
return a;
}else if (n==2){
return matrixMultiply(a,a);
}else if(n > 2 && n % 2 == 0){
return matrixMultiply(matrixPower(a,n/2),matrixPower(a,n/2));
}else{
return matrixMultiply(matrixMultiply(matrixPower(a,(n-1)/2),matrixPower(a,(n-1)/2)),a);
}
}
|
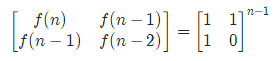
 Ailpay
Ailpay
 Wechat
Wechat